Physics-Based and Data-Driven Models For Robot Control
The project aims at pushing an area of expertise to (i) integrate MBS formulations with data–driven techniques, (ii) develop a hybrid modeling approach for optimal trajectory generation based on the adjoint method, (iii) assess possibilities of practical applications of the developed hybrid models.
Physics-Based and Data-Driven Multibody System Models For Prediction and Feedforward Robot Control (submitted as a project to NCN OPUS)
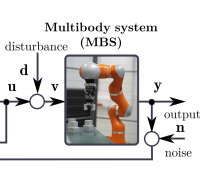
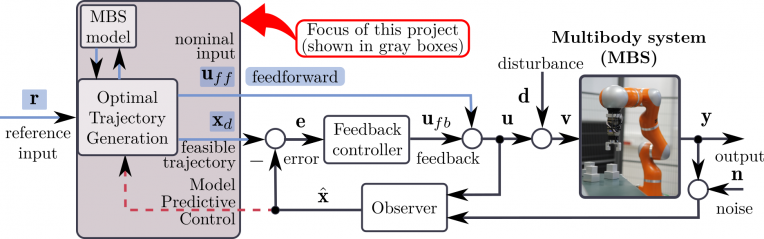
As suggested, the control performance stemming from feedback–feedforward control architecture heavily depends on the quality of MBS models, which predict how control inputs affect the system dynamics. First–principles (e.g., Newton–Euler formalism) and identification techniques can be used to derive multibody or robotic system models. Meanwhile, considerable progress has been achieved using machine learning–based approaches that extract complex dynamical behaviors directly from raw experimental or simulation data.
Moreover, for many robotics systems, the dynamics model derived from first–principles or solely based on data may not be sufficiently accurate, especially in the case of unmodelled nonlinearities (e.g., friction, flexibility). This imprecise model leads to a bad prediction of feedforward control, resulting in significant tracking errors, poor control performances, or even damage to the system. Neither a pure physics–based nor a pure data–driven approach can be considered sufficient for multibody/robotic tasks with high–dimensional state spaces and complex interactions.
These observations imply the recent group’s interest in advancing understanding of the extent to which data–driven paradigms may be combined with pure physics–based models to simulate MBS and generate optimal trajectories. The available state–of–the–art suggests a knowledge gap in this field. Using its previous experience, the group is pushing its area of expertise to (i) integrate MBS formulations with data–driven techniques, (ii) develop a hybrid modeling approach for optimal trajectory generation based on the adjoint method, (iii) assess possibilities of practical applications of the developed hybrid models.