Start » Research » Research projects »
Efficient optimal control methods for multibody systems
Current problems require engineers to predict how specific parameters or control inputs will affect the behavior of the complex multibody system. The adjoint method is one of the more interesting methods for systematically calculating the gradient.
Efficient indirect optimal control methods for multibody systems (Excellence Initiative, Research University in the field of Artificial Intelligence and Robotics, 2020-2022)
Current problems require engineers to predict how specific parameters or control inputs will affect the behavior of the complex multibody system. In the optimal control or design of MBS, an implicit dependency exists between state and design variables, further adding complexity to the problem. This branch of computer-aided engineering is tightly combined with sensitivity analysis, i.e., efficient computation of the derivatives. To this end, various families of methods have been derived, each having its own set of benefits and drawbacks. The adjoint method is one of the more interesting methods for systematically calculating the gradient. The concept behind this approach lies in invoking necessary conditions for the minimum of the optimized functional. Once obtained via variational calculus, these conditions constitute the system adjoint to the dynamic equations of motion – an underlying model of the MBS. Solving the adjoint system yields so-called adjoint variables, allowing for efficient gradient computation. The adjoint method can be applied to such problems as optimal control, optimal design, or parameter identification.
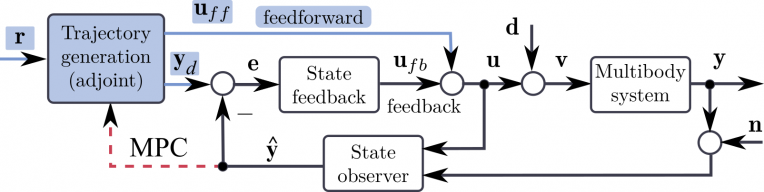
Furthermore, the indirect optimal control methodology provides offline (potentially online) trajectory generation tools that can be utilized as a feedforward signal in the control loop. A recent research project involved a practical implementation of the adjoint method in a feedback-feedforward control architecture. A mathematical model has been derived, composed of an electromechanical device with a five-bar multibody system and two DC motors with a gear transmission. Based on the derived outcome, the input control signal and corresponding trajectory predicted by the model were synthesized. Subsequently, these signals are introduced as reference values to the hardware and compared with classical control algorithms.
The block diagram below presents a model-based control architecture. Symbol r denotes a reference signal that nominally must be enforced. Accordingly, this signal plays the role of an input to the adjoint-based optimization procedure founded on the mathematical model of the MBS. The optimization algorithm yields a control signal uff (theoretically) capable of carrying out the required maneuver. The response generated by the model for uff is depicted as yd, becoming the actual reference trajectory for the system. Due to the discrepancy between the model and the plant, and the presence of disturbances d and measurement noise n, it is required to introduce a feedback loop that generates minor corrections ufb during the execution on the hardware.